Category: randomness

More on the Swiss Franc move

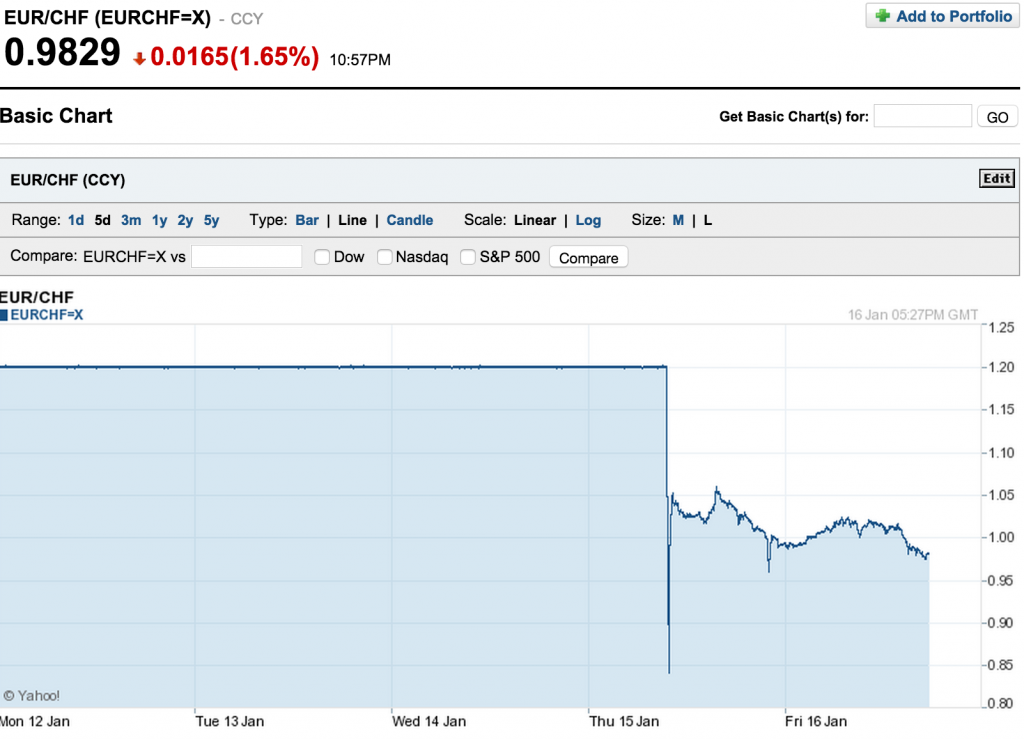
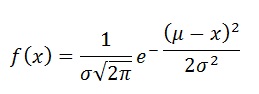The always excellent Matt Levine has reported in Bloomberg (with respect to the recent removal of the cap on the price of the Swiss Franc) that:

Goldman Sachs Chief Financial Officer Harvey Schwartz said on this morning’s earnings call that this was something like a 20-standard-deviation event

While mathematically this might be true, the question is if it makes sense at all. Since it is mathematically easy to model, traders look at volatility of an instrument in terms of its standard deviation. However, standard deviation is a good descriptor of a distribution only if the distribution looks something like a normal distribution. For all other distributions, it is essentially meaningless.

The more important point here is that the movement of the Swiss Franc (CHF) against the Euro had been artificially suppressed in the last three odd years. So from that perspective, whatever Standard Deviation would have been used in order to make the calculation was artificially low and essentially meaningless.

Instead, the way banks ought to have modelled it was in terms of modelling where EUR/CHF would end up in case the cap on the CHF was actually lifted (looking at capital and current flows between Switzerland and the Euro Area, this wouldn’t be hard to model), and then model the probability with which the Swiss National Bank would lift the cap on the Franc, and use the combination of the two to assess the risk in the CHF position. This way the embedded risk of the cap lifting, which was borne out on Thursday, could have been monitored and controlled, and possibly hedged.

There are a couple of other interesting stories connected to the lifting of the cap on the value of the CHF. The first has to do with Alpari, a UK-based FX trading house. The firm has had to declare insolvency following losses from Thursday. And as the company was going insolvent, they put out some interesting quotes. As the Guardian reports:

In the immediate aftermath of Thursday’s move by the Swiss central bank, analysts at Alpari had described the decision as “idiotic” and by Friday the firm had announced it was insolvent. “The recent move on the Swiss franc caused by the Swiss National Bank’s unexpected policy reversal of capping the Swiss franc against the euro has resulted in exceptional volatility and extreme lack of liquidity,” said Alpari.

The second story has to do with homeowners in Hungary and Poland who borrowed their home loans in Swiss Franc, and are now faced with significantly higher payments. I have little sympathy for these homeowners and less sympathy for the bankers who sold them the loans denominated in a foreign currency. I mean, who borrows in a foreign currency to buy a house? I don’t even …

There is a story related to that which is interesting, though. Though Hungary is more exposed to these loans than Poland, it is the Polish banks which are likely to suffer more from the appreciation in the CHF. The irony is that the Hungarian market was initially much more loosely regulated compared to the Polish market, where only wealthier people were allowed to borrow in CHF. But in Hungary, the regulator took more liberties in terms of forcing banks to take the hit on the exchange rate movement, and the loans were swapped back into the local currency a while back.

In related reading, check out this post by my Takshashila colleague Anantha Nageswaran on the crisis. I agree with most of it.

 

Pakistan, Swiss Franc and the costs of suppressing volatility

Back in 2008, during the CDO/MBS/Lehman/… induced financial crisis (and also a time of domestic political crisis in Pakistan since Musharraf had just resigned),  Pakistan set a funny rule – they ruled that stock prices could not fall below a particular limit. So there was no trading, since the crisis meant that no one wanted to buy shares at prevailing prices. And then after a long time the ban got lifted. And shares promptly fell. Check out the graph of the MSCI Index for Pakistan from that time here (from FT):

Check out the late 2008 period when shares were virtually flat. And then the fall after that

Sometime back, Switzerland decided that its Franc was appreciating too much and put a ceiling on its price by pegging it to the Euro. The Franc can be worth no more than five-sixth of a Euro, they decreed. And the Franc stayed flat, close to the limit. And then in a sudden move yesterday, following instability in the Eurozone which meant the Euro has been getting considerably weaker, the Swiss National Bank decided that continuing to maintain the peg was costly. And they pulled the plug on the peg (couldn’t resist the alliteration). The graph is here, snapped off Yahoo Finance (took screenshot since I couldn’t figure out how to embed it):

This graph shows the number of Euros per Swiss Franc. There was a floor of 1.2 till 14/1/15 which was suddenly removed on 15/1/15

I chose the 5-day chart since on any longer horizon yesterday’s drop was hardly visible. With time, once we have a longer time scale available, we will see that this graph will again start looking like the Pakistan graph.

Thanks to the sudden appreciation in the CHF,  there has been bloodbath in the markets. Some FX traders have gone down. Alpari has declared itself insolvent. Global Brokers NZ is closing down. US-based FX trader FXCM is in trouble. And there could be lots of trouble in Poland where people took home loans denominated in CHF (this might sound heartless but such utter stupidity – like taking a home loan in a foreign currency – deserves to be punished).

The broader point I’m trying to make here is a paraphrasing of the old adage “still waters run deep”. When something seems unusually quiet, either held in place unnaturally or even if there is no apparent force holding it in place unnaturally, it is usually a sign that when the floodgates open much will get washed away (apologies for the surfeit of metaphor in this paragraph). When you suppress “local volatility”, the suppressed entropy builds, and when there comes a time that it can be suppressed no more, it acts with such force that there will be much damage.

As Nassim Nicholas Taleb argues in the black swan (link to my paraphrasing of his argument), countries with short-term political instability such as Italy or India or Japan are much less likely to face any major political instability. On the other hand, countries like China, he argues, where small instability has been artificially held down, when instability hits, it will hit in a way that it will hurt real bad.

I’ll end this post with a page from Taleb’s first book Dynamic Hedging, which he tweeted earlier today (I haven’t read it but want to read it but haven’t been able to procure it). Read and enjoy:

 

Good things do happen to those who wait

So once again I’ve taken myself off Twitter and Facebook. After a three-month sabbatical which ended a month back, I was back on these two social networks in a “limited basis” – I had not installed the apps on my phone and would use them exclusively from my computer. But as days went by, I realised I was getting addicted once again, and losing plenty of time just checking if someone had replied to any of the wisecracks I had put on some of those. So I’ve taken myself off once again, this time for at least one month.

This post is about the last of my wisecracks on facebook before I left it. A facebook friend had put an update that said “good things do happen to those who wait”. I was in a particularly snarky mood, and decided to call out the fallacy and left the comment below.

Good things

In hindsight I’m not sure if it was a great decision – perhaps something good had happened to the poor guy after a really long time, and he had decided to celebrate it by means of putting this cryptic message. And I, in my finite wisdom, had decided to prick his balloon by spouting gyaan. Just before I logged out of facebook this morning, though, I checked and found that he had liked my comment, though I don’t know what to make of it.

Earlier this year I had met an old friend for dinner, and as we finished and were walking back to the mall parking lot, he asked for my views on religion. I took a while to answer, for I hadn’t given thought to the topic for a while. And then it hit me, and I told him, “once I started appreciating that correlation doesn’t imply causation, it’s very hard for me to believe in religion”. Thinking about it now, a lot of other common practices, which go beyond religion, are tied to mistaking correlation for causation.

Take, for example, the subject of the post. “Good things happen to those who wait”, they say. It is basically intended as encouragement for people who don’t succeed in the first few attempts. What it doesn’t take care of it that the failures in the first few attempts might be “random”, or that even success when it does happen is the result of a random process.

Say, for example, you are trying to get a head upon the toss of a coin. You expect half a chance of a head the first time. It disappoints. You assume the second time the chances should be better, since it didn’t work out the first time (you don’t realise the events are independent), and are disappointed again. A few more tails and disappointment turns to disillusionment, and you start wondering if the coin is fair at all. Finally, when you get a head, you think it is divine retribution for having waited, and say that “good things happen to those who wait”.

In your happiness that you finally got a head, what you assume is that repeated failure on the first few counts actually push up your chance of getting your head, and that led to your success on the Nth attempt. What you fail to take into account is that there was an equal chance (assuming a fair coin) of getting a tail on the Nth attempt also (which you would have brushed off, since you were used to it).

In my comment above I’ve said “selection bias” but I’m not sure if that’s the right terminology – essentially when things go the way you want them to, you take notice and ascribe credit, but when things don’t go the way you want you don’t notice.

How many times have you heard people going through a happy experience saying they’re going through it “by God’s grace?”. How many times have you heard people curse God for not listening to their prayers when they’re going through a bad patch? Hardly? Instead, how many times have you heard people tell you that God is “testing them” when they’re going through a bad patch?

It’s the same concept of letting your priors (you see God as a good guy who will never harm you) affect the way you see a certain event. So in my friend’s case above, after a few “tails” he had convinced himself that “good things do happen to those who wait” and was waiting for a few more coin tosses until he finally sprang a head and announced it to the world!

Now I remember: I think it’s called confirmation bias.

Doctors and correlation-causation

One of the common cribs about the medical profession is that most doctors don’t have enough grounding in mathematics and statistics (subjects they typically don’t study beyond high school). Given the role of mathematics and statistics in medicine, in terms of gathering evidence, medical testing, etc. the lack of mathematical or statistical knowledge can have serious consequences in terms of interpretation of techniques and symptoms and all that.

In the field of statistics we have this adage that goes that we should “treat the disease and not the symptom”. This is no less true in the medical profession – let’s say that you have a bacterial infection which causes a fever, a poor doctor would diagnose your fever by taking your temperature, assume that it is the fever thanks to which you are sick and give you medication to lower the fever without realising that there is a “third variable” that might be causing both – your fever and your sickness. Thus, your fever might come down and consequently your sickness but both would presently appear.

I’ve had chronic pain in my heels for a few months now. It’s especially severe whenever I put my feet on the ground from a raised position. Someone had told me that it occurs due to calcification near the Achilles Tendon, and I must take medication for that. Having pushed it for a few months now I finally went to see my uncle who is an orthopaedic yesterday (this is the same guy who told me about my Boxer’s Fist).

He promptly diagnosed me with Plantar Fasciitis, and wrote down some medication, and told me what I need to do in order to reduce the pain in my feet. After a short conversation on what else I need to do, and any precautions, and all such, I asked him about the calcification thingy – whether he had ruled out that calcification of the Achilles Tendon was causing this problem.

“I’m sure there will be some calcification”, he said, “and I’m not sending you for an X-ray because I have a very good idea of what it will show and it won’t add much value”. And then he proceeded to explain that calcification is a “result” of plantar fasciitis and not a cause of it. He didn’t use the terms “correlation” or “causation” but he explained that when you suffer from plantar fasciitis you end up with both calcification of your Achilles Tendon and also shooting pain in your heels, especially immediately after waking up. The two are thus related, he said, but neither causes the other, but there is a third factor (fasciitis) that causes both, and that is the one that he is treating me for!

I was doubly impressed with him – first for understanding “information theory” in terms of understanding that the X-ray wouldn’t add much information, and secondly for recognising that there was a third factor and that correlation should not be mistaken for causation. Or perhaps I had a particularly low prior for mathematical and statistical skills of doctors!

Postscript

He refused to charge me a fee, since I’m his nephew. While on my way out I was thinking about it and wondering on what circumstances I would waive my professional fees for my consulting. And I realised it would be hard to do so for anyone! It made me wonder what made my uncle waive his medical fees, while I’m extremely unlikely to do that.

I realised it has to do with the investment. He spent about five to ten minutes with me (perhaps a bit longer), but essentially his marginal cost of treating me was quite low. And this was a marginal cost that he was willing to sacrifice in return for the goodwill he gets for treating the extended family for free. Considering the size of my engagements, though, the marginal cost is usually high and is seldom justified by goodwill!

Sigma and normal distributions

I’m in my way to the Bangalore airport now, north of hebbal flyover. It’s raining like crazy again today – the second time in a week it’s raining so bad.

I instinctively thought “today is an N sigma day in terms of rain in Bangalore” (where N is a large number). Then I immediately realized that such a statement would make sense only if rainfall in Bangalore were to follow a normal distribution!

When people normally say something is an N sigma event what they’re really trying to convey is that it is a very improbable event and the N is a measure of this improbability. The relationship between N and the improbability implied is given by the shape of the normal curve.

However when a quantity follow a distribution other than normal the relationship between the mean and standard deviation (sigma) and the implied probability breaks down and the number of sigmas will mean something totally different in terms of the implied improbability.

It is good practice, thus, to stop talking in terms of sigma and talk in terms of of odds. It’s better to say “a one in forty event” rather than saying “two sigma event” (I’m assuming a one tailed normal distribution here).

The broader point is that the normal distribution is too ingrained in people’s minds which leads then to assume all quantities follow a normal distribution – which is dangerous and needs to be discouraged strongly.

In this direction any small measure – like talking odds rather than in terms of sigma – will go a long way!

Why Brazil is undervalued by punters

When India exited the 2007 Cricket World Cup, broadcasters, advertisers and sponsors faced huge losses. They had made the calculations for the tournament based on the assumption that India would qualify for the second group stage, at least, and when India failed to do so, it possibly led to massive losses for these parties.

Back then I had written this blog post where I had explained that one way they could have hedged their exposure to the World Cup would have been by betting against India’s performance. Placing a bet that India would not get out of their World Cup group would have, I had argued, helped mitigate the potential losses coming out of India’s early exist. It is not known if any of them actually hedged their World Cup bets in the betting market.

Looking at the odds in the ongoing Football World Cup, though, it seems like bets are being hedged. The equivalent in the World Cup is Brazil, the home team. While the world football market is reasonably diversified with a large number of teams having a reasonable fan following, the overall financial success of the World Cup depends on Brazil’s performance. An early exit by Brazil (as almost happened on Saturday) can lead to significant financial losses for investors in the tournament, and thus they would like to hedge these bets.

The World Cup simulator is a very interesting website which simulates the remaining games of the World Cup based on a chosen set of parameters (you can choose a linear combination of Elo rating, FIFA ranking, ESPN Soccer Power Index, Home advantage, Players’ Age, Transfer values, etc.). This is achieved by means of a Monte Carlo simulation.

I was looking at this system’s predictions for the Brazil-Colombia quarter final, and comparing that with odds on Betfair (perhaps the most liquid betting site). Based purely on Elo rating, Brazil has a 77% chance of progress. Adding home advantage increases the probability to 80%. The ESPN SPI is not so charitable to Brazil, though – it gives Brazil a 65% chance of progress, which increases to 71% when home advantage is factored in.

Assuming that home advantage is something that cannot be ignored (though the extent of it is questionable for games played at non-traditional venues such as Fortaleza or Manaus), we will take the with home advantage numbers – that gives a 70-80% chance of Brazil getting past Colombia.

So what does Betfair say? As things stand now, a Brazil win is trading at 1.85, which translates to a 54% chance of a Brazil victory.  A draw is trading at 3.8, which translates to a 26% chance. Assuming that teams are equally matched in case of a penalty shootout, this gives Brazil a 67% chance of qualification – which is below the range that is expected based on the SPI and Elo ratings. This discount, I hypothesize, is due to the commercial interest in Brazil’s World Cup performance.

Given that a large number of entities stand to gain from Brazil’s continued progress in the World Cup, they would want to protect their interest by hedging their bets – or by betting against Brazil. While there might be some commercial interest in betting against Colombia (by the Colombian World Cup broadcaster, perhaps?) this interest would be lower than that of the Brazil interest. As a result, the volume of “hedges” by entities with an exposure to Brazil is likely to pull down the “price” of a Brazil win – in other words, it will lead to undervaluation (in the betting market) of the probability that Brazil will win.

So how can you bet on it? There is no easy answer – since the force is acting only one way, there is no real arbitrage opportunity (all betting exchanges are likely to have same prices). The only “trade” here is to go long Brazil – since the “real probability” or progress is probably higher than what is implied by the betting markets. But then you need to know that this is a directional bet contingent upon Brazil’s victory, and need to be careful!

The Signficicance of Statistical Significance

Last year, an aunt was diagnosed with extremely low bone density. She had been complaining of back pain and weakness, and a few tests later, her orthopedic confirmed that bone density was the problem. She was put on a course of medication, and then was given by shots. A year later, she got her bone density tested again, and found that there was not much improvement.

She did a few rounds of the doctors again – orthopedics, endocrinologists and the like, and the first few were puzzled that the medication and the shots had had no effect. One of the doctors, though, saw something others didn’t – “there is no marked improvement, for sure”, he remarked, “but there is definitely some improvement”.

Let us say you take ten thousand observations in “state A”, and another ten thousand in “state B”. The average of your observations in state A is 100, and the standard deviation is 10. The average of your observations in state B is 101, and the standard deviation is 10. Is there a significant difference between the observations in the two states?

Statistically speaking, there most definitely is (with 10000 samples, the “standard error” given a standard deviation of 10 is 0.1 (10 / sqrt(10000) ), and the two sets of observations are ten standard errors apart which means that the difference between them is “statistically significant” to a high degree of significance. The question, however, is if the difference is actually “significant” (in the non-statistical sense of the word).

Think about it from the context of drug testing. Let us say that we are testing a drug for increasing bone density among people with low bone density (like my aunt). Let’s say we catch 10000 mice and measure their bone densities. Let’s say the average is 100, with a standard deviation of 10.

Now, let us inject our drug (in the appropriate dosage – scaled down from man to mouse) on our mice, and after they’ve undergone the requisite treatment, measure the bone densities again. Let’s say that the average is now 101, with a standard deviation of 10. Based on this test, can we conclude that our drug is effective for improving bone density?

What cannot be denied is that one course of medication among mice produces results that are statistically significant – there is an increase in bone density among mice that cannot be explained by randomness alone. From this perspective, the drug is undoubtedly effective – that there is a positive effect from taking the drug is extremely highly likely.

However, does this mean that we use this drug for treating low bone density? Despite the statistical significance, the answer to this is not very clear. Let us for a moment assume that there are no competitors – there is no other known drug which can increase a patient’s bone density by a statistically significant amount. So the choice is this – we either not use any drug, leading to no improvement in the patient (let us assume that another experiment has shown that in the absence of drugging, there is no change in bone density) or we use this drug, which produces a small but statistically significant improvement. What do we do?

The question we need to answer here is whether the magnitude of improvement on account of taking this drug is worth the cost (monetary cost, possible side effects, etc.) of taking the drug. Do we want to put the patient through the trouble of taking the medication when we know that the difference it will make, though statistically significant, is marginal? It is a fuzzy question, and doesn’t necessarily have a clear answer.

In summary, the basic point is that a statistically significant improvement does not mean that the difference is significant in terms of magnitude. With samples large enough, even small changes can be statistically significant, and we need to be cognizant of that.

Postscript
No mice were harmed in the course of writing this blog post

The NRN premium is over

With the resignation of Infosys President BG Srinivas and the subsequent drop in the share price in the markets today, the NR Narayana Murthy premium on the Infosys stock is over. Ironically, this happens almost exactly a year since NRN made a comeback to the company in an executive capacity.

The figure below charts how the Infosys stock and the market index (Nifty ) have moved in the last one year. In order to compare the two, we have indexed their prices as of 30th May 2013, just before NRN’s return was announced (the announcement was made as of 2nd June, but the sharp spike in Infy on 31st May 2013, when the broad market fell, can be attributed to insider trading by people in the know), to 100. Notice how the Infosys stock soared in the six months after NRN’s return. In January and February, the stock traded at a 60% premium to its pre-NRN value, while the nifty was practically flat till then.

infy1

And then things started dropping. Even when the broad markets rose in March-April this year, Infosys continued to fall. The rally in early-mid May took it along, but now the stock has fallen again. This morning (latest data as of noon), the stock has fallen by about 6% thanks to Srinivas’s departure, and we can see that the gap between Infy and the market has really narrowed.

Next, we look at the ratio of the Infy price to the market index. Again we index it to 100 as of 30th May 2013. This graph shows the premium in the Infy share price over the last year. Notice that for the first time, the premium has fallen below 10% (it’s currently 7%). 

infy2

 

Finally, we will compare the Infy stock to the CNX IT index, which tracks the sector (that way, any sectoral premium in Infy can be extracted out). Again, we will plot the relative values of Infy to the CNX IT index, indexed to 100 as of 30th May 2013.

infy3

This graph looks like no other. What this tells us is that whatever premium Infosys enjoys over the broad market is a function of the sector, and that ever since the sharp drop in early March (on account of weak results), the NRN premium on the Infy stock relative to the sector has disappeared. As of now, compared to the sector, Infy is at an all time low.

Finally, a regression. If we regress infy stock returns against the returns in the IT index and Nifty, what we find is that Nifty returns hardly affect Infosys returns (R^2 of 7%), while the IT Index returns explain about 76% of Nifty returns. When regressed against both, Nifty returns come out as insignificant and the R^2 remains at 76%.

Putting all these statistics aside, however, the message is simple – the NRN premium on the Infy stock is over.

 

 

Standard deviation is over

I first learnt about the concept of Standard Deviation sometime in 1999, when we were being taught introductory statistics in class 12. It was classified under the topic of “measures of dispersion”, and after having learnt the concepts of “mean deviation from median” (and learning that “mean deviation from mean” is identically zero) and “mean absolute deviation”, the teacher slipped in the concept of the standard deviation.

I remember being taught the mnemonic of “railway mail service” to remember that the standard deviation was “root mean square” (RMS! get it?). Calculating the standard deviation was simple. You took the difference between each data point and the average, and then it was “root mean square” – you squared the numbers, took the arithmetic mean and then square root.

Back then, nobody bothered to tell us why the standard deviation was significant. Later in engineering, someone (wrongly) told us that you square the deviations so that you can account for negative numbers (if that were true, the MAD would be equally serviceable). A few years later, learning statistics at business school, we were told (rightly this time) that the standard deviation was significant because it doubly penalized outliers. A few days later, we learnt hypothesis testing, which used the bell curve. “Two standard deviations includes 95% of the data”, we learnt, and blindly applied to all data sets – problems we encountered in examinations only dealt with data sets that were actually normally distributed. It was much later that we figured that the number six in “six sigma” was literally pulled out of thin air, as a dedication to Sigma Six, a precursor of Pink Floyd.

Somewhere along the way, we learnt that the specialty of the normal distribution is that it can be uniquely described by mean and standard deviation. One look at the formula for its PDF tells you why it is so:

Most introductory stats lessons are taught from the point of view of using stats to do science. In the natural world, and in science, a lot of things are normally distributed (hence it is the “normal” distribution). Thus, learning statistics using the normal distribution as a framework is helpful if you seek to use it to do science. The problem arises, however, if you assume that everything is normally distributed, as a lot of people do when they learn deep statistics using the normal distribution.

When you step outside the realms of natural science, however, you are in trouble if you were to blindly use the standard deviation, and consequently, the normal distribution. For in such realms, the normal distribution is seldom normal. Take, for example, stock markets. Most popular financial models assume that the movement of the stock price is either normal or log-normal (the famous Black-Scholes equation uses the latter assumption). In certain regimes, they might be reasonable assumptions, but pretty much anyone who has reasonably followed the markets knows that stock price movements have “fat tails”, and thus the lognormal assumption is not a great example.

At least the stock price movement looks somewhat normal (apart from the fat tails). What if you are doing some social science research and are looking at, for example, data on people’s incomes? Do you think it makes sense at all to define standard deviation for income of a sample of people? Going further, do you think it makes sense at all to compare the dispersion in incomes across two populations by measuring the standard deviations of incomes in each?

I was once talking to an organization which was trying to measure and influence salesperson efficiency. In order to do this, again, they were looking at mean and standard deviation. Given that the sales of one salesperson can be an order of magnitude greater than that of another (given the nature of their product), this made absolutely no sense!

The problem with the emphasis on standard deviation in our education means that most people know one way to measure dispersion. When you know one method to measure something, you are likely to apply it irrespective of whether it is the appropriate method to use given the circumstances. It leads to the proverbial hammer-nail problem.

What we need to understand is that the standard deviation makes sense only for some kinds of data. Yes, it is mathematically defined for any set of numbers, but it makes physical sense only when the data is approximately normally distributed. When data doesn’t fit such a distribution (and more often than not it doesn’t), the standard deviation makes little sense!

For those that noticed, the title of this post is a dedication to Tyler Cowen’s recent book.