Tag: sample size

69 is the answer

The IDFC-Duke-Chicago survey that concluded that 50% of Bangalore had covid-19 in late June only surveyed 69 people in the city. 

When it comes to most things in life, the answer is 42. However, if you are trying to rationalise the IDFC-Duke-Chicago survey that found that over 50% of people in Bangalore had had covid-19 by end-June, then the answer is not 42. It is 69.

For that is the sample size that the survey used in Bangalore.

Initially I had missed this as well. However, this evening I attended half of a webinar where some of the authors of the survey spoke about the survey and the paper, and there they let the penny drop. And then I found – it’s in one small table in the paper.

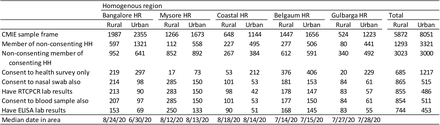
The IDFC-Duke-Chicago survey only surveyed 69 people in Bangalore

The above is the table in its glorious full size. It takes effort to read the numbers. Look at the second last line. In Bangalore Urban, the ELISA results (for antibodies) were available for only 69 people.

And if you look at the appendix, you find that 52.5% of respondents in Bangalore had antibodies to covid-19 (that is 36 people). So in late June, they surveyed 69 people and found that 36 had antibodies for covid-19. That’s it.

To their credit, they didn’t highlight this result (I sort of dug through their paper to find these numbers and call the survey into question). And they mentioned in tonight’s webinar as well that their objective was to get an idea of the prevalence in the state, and not just in one particular region (even if it be as important as Bangalore).

That said, two things that they said during the webinar in defence of the paper that I thought I should point out here.

First, Anu Acharya of MapMyGenome (also a co-author of the survey) said “people have said that a lot of people we approached refused consent to be surveyed. That’s a standard of all surveying”. That’s absolutely correct. In any random survey, you will always have an implicit bias because the sort of people who will refuse to get surveyed will show a pattern.

However, in this particular case, the point to note is the extremely high number of people who refused to be surveyed – over half the households in the panel refused to be surveyed, and in a further quarter of the panel households, the identified person refused to be surveyed (despite the family giving clearance).

One of the things with covid-19 in India is that in the early days of the pandemic, anyone found having the disease would be force-hospitalised. I had said back then (not sure where) that hospitalising asymptomatic people was similar to the “precogs” in Minority Report – you confine the people because they MIGHT INFECT OTHERS.

For this reason, people didn’t want to get tested for covid-19. If you accidentally tested positive, you would be institutionalised for a week or two (and be made to pay for it, if you demanded a private hospital). Rather, unless you had clear symptoms or were ill, you were afraid of being tested for covid-19 (whether RT-PCR or antibodies, a “representative sample” won’t understand).

However, if you had already got covid-19 and “served your sentence”, you would be far less likely to be “afraid of being tested”. This, in conjunction with the rather high proportion of the panel that refused to get tested, suggests that there was a clear bias in the sample. And since the numbers for Bangalore clearly don’t make sense, it lends credence to the sampling bias.

And sample size apart, there is nothing Bangalore-specific about this bias (apart from that in some parts of the state, the survey happened after people had sort of lost their fear of testing). This further suggests that overall state numbers are also an overestimate (which fits in with my conclusion in the previous blogpost).

The other thing that was mentioned in the webinar that sort of cracked me up was the reason why the sample size was so low in Bangalore – a lockdown got announced while the survey was on, and the sampling team fled. In today’s webinar, the paper authors went off on a rant about how surveying should be classified as an “essential activity”.

In any case, none of this matters. All that matters is that 69 is the answer.

 

Randomness and sample size

I have had a strange relationship with volleyball, as I’ve documented here. Unlike in most other sports I’ve played, I was a rather defensive volleyball player, excelling in backline defence, setting and blocking, rather than spiking.

The one aspect of my game which was out of line with the rest of my volleyball, but in line with my play in most other sports I’ve played competitively, was my serve. I had a big booming serve, which at school level was mostly unreturnable.

The downside of having an unreturnable serve, though, is that you are likely to miss your serve more often than the rest – it might mean hitting it too long, or into the net, or wide. And like in one of the examples I’ve quoted in my earlier post, it might mean not getting a chance to serve at all, as the warm up serve gets returned or goes into the net.

So I was discussing my volleyball non-career with a friend who is now heavily involved in the game, and he thought that I had possibly been extremely unlucky. My own take on this is that given how little I played, it’s quite likely that things would have gone spectacularly wrong.

Changing domains a little bit, there was a time when I was building strategies for algorithmic trading, in a class known as “statistical arbitrage”. The deal there is that you have a small “edge” on each trade, but if you do a large enough number of trades, you will make money. As it happened, the guy I was working for then got spooked out after the first couple of trades went bad and shut down the strategy at a heavy loss.

Changing domains a little less this time, this is also the reason why you shouldn’t check your portfolio too often if you’re investing for the long term – in the short run, when there have been “fewer plays”, the chances of having a negative return are higher even if you’re in a mostly safe strategy, as I had illustrated in this blog post in 2008 (using the Livejournal URL since the table didn’t port well to wordpress).

And changing domains once again, the sheer number of “samples” is possibly one reason that the whole idea of quantification of sport and “SABRmetrics” first took hold in baseball. The Major League Baseball season is typically 162 games long (and this is before the playoffs), which means that any small edge will translate into results in the course of the league. A smaller league would mean fewer games and thus more randomness, and a higher chance that a “better play” wouldn’t work out.

This also explains why when “Moneyball” took off with the Oakland A’s in the 1990s, they focussed mainly on league performance and not performance in the playoffs – in the latter, there are simply not enough “samples” for a marginal advantage in team strength to necessarily have the impact in terms of results.

And this is the problem with newly appointed managers of elite football clubs in Europe “targeting the Champions League” – a knockout tournament of that format means that the best team need not always win. Targeting a national league, played out over at least 34 games in the season is a much better bet.

Finally, there is also the issue of variance. A higher variance in performance means that observations of a few instances of bad performance is not sufficient to conclude that the player is a bad performer – a great performance need not be too far away. For a player with less randomness in performance – a more steady player, if you will – a few bad performances will tell you that they are unlikely to come good. High risk high return players, on the other hand, need to be given a longer rope.

I’d put this in a different way in a blog a few years back, about Mitchell Johnson.

The Signficicance of Statistical Significance

Last year, an aunt was diagnosed with extremely low bone density. She had been complaining of back pain and weakness, and a few tests later, her orthopedic confirmed that bone density was the problem. She was put on a course of medication, and then was given by shots. A year later, she got her bone density tested again, and found that there was not much improvement.

She did a few rounds of the doctors again – orthopedics, endocrinologists and the like, and the first few were puzzled that the medication and the shots had had no effect. One of the doctors, though, saw something others didn’t – “there is no marked improvement, for sure”, he remarked, “but there is definitely some improvement”.

Let us say you take ten thousand observations in “state A”, and another ten thousand in “state B”. The average of your observations in state A is 100, and the standard deviation is 10. The average of your observations in state B is 101, and the standard deviation is 10. Is there a significant difference between the observations in the two states?

Statistically speaking, there most definitely is (with 10000 samples, the “standard error” given a standard deviation of 10 is 0.1 (10 / sqrt(10000) ), and the two sets of observations are ten standard errors apart which means that the difference between them is “statistically significant” to a high degree of significance. The question, however, is if the difference is actually “significant” (in the non-statistical sense of the word).

Think about it from the context of drug testing. Let us say that we are testing a drug for increasing bone density among people with low bone density (like my aunt). Let’s say we catch 10000 mice and measure their bone densities. Let’s say the average is 100, with a standard deviation of 10.

Now, let us inject our drug (in the appropriate dosage – scaled down from man to mouse) on our mice, and after they’ve undergone the requisite treatment, measure the bone densities again. Let’s say that the average is now 101, with a standard deviation of 10. Based on this test, can we conclude that our drug is effective for improving bone density?

What cannot be denied is that one course of medication among mice produces results that are statistically significant – there is an increase in bone density among mice that cannot be explained by randomness alone. From this perspective, the drug is undoubtedly effective – that there is a positive effect from taking the drug is extremely highly likely.

However, does this mean that we use this drug for treating low bone density? Despite the statistical significance, the answer to this is not very clear. Let us for a moment assume that there are no competitors – there is no other known drug which can increase a patient’s bone density by a statistically significant amount. So the choice is this – we either not use any drug, leading to no improvement in the patient (let us assume that another experiment has shown that in the absence of drugging, there is no change in bone density) or we use this drug, which produces a small but statistically significant improvement. What do we do?

The question we need to answer here is whether the magnitude of improvement on account of taking this drug is worth the cost (monetary cost, possible side effects, etc.) of taking the drug. Do we want to put the patient through the trouble of taking the medication when we know that the difference it will make, though statistically significant, is marginal? It is a fuzzy question, and doesn’t necessarily have a clear answer.

In summary, the basic point is that a statistically significant improvement does not mean that the difference is significant in terms of magnitude. With samples large enough, even small changes can be statistically significant, and we need to be cognizant of that.

Postscript
No mice were harmed in the course of writing this blog post