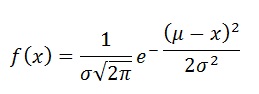One silver lining in the madness of the US Presidential election counting is that there are some interesting analyses floating around regarding polling and surveying and probabilities and visualisation. Take this post from Andrew Gelman’s blog, for example:
Suppose our forecast in a certain state is that candidate X will win 0.52 of the two-party vote, with a forecast standard deviation of 0.02. Suppose also that the forecast has a normal distribution.[…]
Then your 68% predictive interval for the candidate’s vote share is [0.50, 0.54], and your 95% interval is [0.48, 0.56].
Now suppose the candidate gets exactly half of the vote. Or you could say 0.499, the point being that he lost the election in that state.
This outcome falls on the boundary of the 68% interval, it’s one standard deviation away from the forecast. In no sense would this be called a prediction error or a forecast failure.
But now let’s say it another way. The forecast gave the candidate an 84% chance of winning! And then he lost. That’s pretty damn humiliating. The forecast failed.
It took me a while to appreciate this. In a binary outcome, if your model says predicts 52%, with a standard deviation of 2%, you are in effect predicting a “win” (50% or higher) with a probability of 84%! Somehow I had never thought about it that way.
In any case, this tells you how tricky forecasting a binary outcome is. You might think (based on your sample size) that a 2% standard deviation is reasonable. Except that when the mean of your forecast is close to the barrier (50% in this case), the “reasonable standard deviation” lends a much stronger meaning to your forecast.
Gelman goes on:
That’s right. A forecast of 0.52 +/- 0.02 gives you an 84% chance of winning.
We want to increase the sd in the above expression so as to send the win probability down to 60%. How much do we need to increase it? Maybe send it from 0.02 to 0.03?
> pnorm(0.52, 0.50, 0.03) [1] 0.75Uh, no, that wasn’t enough! 0.04?
> pnorm(0.52, 0.50, 0.04) [1] 0.690.05 won’t do it either. We actually have to go all the way up to . . . 0.08:
> pnorm(0.52, 0.50, 0.08) [1] 0.60That’s right. If your best guess is that candidate X will receive 0.52 of the vote, and you want your forecast to give him a 60% chance of winning the election, you’ll have to ramp up the sd to 0.08, so that your 95% forecast interval is a ridiculously wide 0.52 +/- 2*0.08, or [0.36, 0.68].
Who said forecasting an election is easy?