growth – Pertinent Observations

Relative size of hand and mouth

So the daughter and I are playing a game where she makes a gesture and I try to imitate it (this blogpost is not part of the game, of course). Like me, and my mother before me, she’s an expert in contorting her face in all kinds of ways. So it is a fun game, to try and imitate each other in the way we contort faces.

One thing she does which I’m thoroughly incapable of replicating, however, is putting hands in mouth. She seems well capable of inserting her whole hand inside her mouth. On the other hand I struggle to even put in a finger or two.

This makes me wonder about the relative growth patterns in hands and mouths. As a baby, we are born with big heads and faces, and consequently big mouths. Limbs are tiny in comparison. As we grow, though, our limbs grow much faster than our heads, to the effect that soon we become incapable of putting hands in our mouths, and at best, can just suck on a thumb!

Another thing I’ve noticed in my daughter’s growing up is that she seems thoroughly incapable of putting her big toes in her mouth. It’s a well documented fact (with photos) that I used to do a fair amount of this as a baby. Even now, with some effort I can bring around my big toe and can suck on it if I want to. The daughter, however, seems thoroughly incapable of doing that.

Conventional wisdom is that as we grow older our bodies become less flexible. I wonder if it’s actually a curve that first increases, hits a maximum and then decreases slowly through life. So maybe my daughter can’t suck on her big toe because she’s too small for it (she’s three months old now)!

Whatever it is, it’s fascinating to watch babies grow!

On 2ab, Communal Harmony and Economic Growth

I’ve used the concept of “2ab” once before, a day after the Prime Minister used the term in a much lampooned remark, to explain why we need Net Neutrality. I turn to the same concept again to explain why communal harmony is necessary for economic growth.

Some 4-5 days back, a mob entered the house of one Muslim guy who was allegedly cooking beef, and lynched him to death. In response, rather than booking the mob, the police sent meat sample from the victim’s house to “test if he was actually cooking beef” – as if its confirmation as beef would justify the murder.

I’ve mostly been off social media (and hence not fully following the story) since then, but RSS leader Tarun Vijay hasmade some remarks about “lynching on suspicion being wrong“, and star Indian Express columnist Pratap Bhanu Mehta has laid the blame at the Prime Minister’s feet. Mehta writes (HT: V Anantha Nageswaran):

The blame for this has to fall entirely on Modi. Those who spread this poison enjoy his patronage. This government has set a tone that is threatening, mean-spirited and inimical to freedom. Modi should have no doubt that he bears responsibility for the poison that is being spread by the likes of Culture Minister Mahesh Sharma and Vijay — whether through powerlessness or design is irrelevant. But we can be grateful to Vijay for reminding us that the threat to India’s soul emanates from the centre of power, almost nowhere else. It is for that centre, and Modi in particular, to persuade us otherwise.

Now there were two kinds of people Modi appealed to when he came to power in a resounding victory last year – bigots and aspirers. The former hoped that Modi would “teach a lesson to the Muslims”. The latter hoped that Modi would help accelerate economic growth, after a mostly useless and scam-ridden UPA2 government. And Modi might have thought that these two goals are compatible (else it would make no sense to court these two constituencies). Even in theory they are not.

The Gross Domestic Product (GDP), whose growth rate is seen as a bellwether of the economy’s performance, is a measure of the amount of trade. Trade can be external (let’s set that aside for now) and internal. There are many factors that determine the extent of internal trade (trade between the people of the country), but at the margin, it is proportional to the number of possible pairs of people who can trade with each other.

In other words, trade is another of those quantities that follows Metcalfe’s Law, and depends on strong network effects. If the number of people in a place (region or country or state or city) is 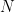$N$ , and if everyone can trade with one another, the number of possible trading relationships is $N^2$ .

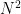Despite the development of the rule of law and Contract Acts and court-brokered dispute settlements, people typically trade with other people they can trust. In the past, this meant that certain families or communities had a monopoly over trade. Over time, with the development of laws and contracts and courts, this has expanded. Yet, people still hesitate to trade with people they don’t trust.

So what happens when there is communal or caste disharmony? Then you will not trust someone who belongs to another caste or community or religion because of the person’s community (and notwithstanding the person’s personal characteristics). And if you don’t trust them, you don’t trade with them. And what does this mean for the total volume of trade?

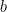It’s time to bring out our $(a+b)^2$ expansion. If you have two communities of sizes $a$ and $b$ , in the absence of trust between the communities, the total trade in the community is ceteris paribus proportional to 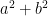$a^2 + b^2$ . If the two communities live harmoniously and have enough mutual trust that communal differences have no bearing on trade, the total trade in the community is ceteris paribus proportional to $(a+b)^2$ . The difference between the two? 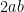$2ab$ of course!

Communal distrust and the lack of communal harmony ends up restricting the number of possible trading partners for each person, and thus we lose out in terms of the correlation term. In other words, bigotry costs us in terms of GDP growth.

Lastly, even if the government of the day is concerned more about the welfare of one particular community over another, communal harmony makes sense. For by creating distrust, people belonging to the government’s favourite community are denied trade with people of the less favoured community. And this adversely impacts the more favoured community!

Certainty in monetary policy

Two big takeaways from today’s monetary policy review are the institution of a formal inflation target and a commitment to consistency in monetary policy

I found two major takeaways from RBI Governor Raghuram Rajan’s press conference this morning following the RBI policy review (where both the policy rate and the cash reserve ratio were held constant).

Firstly, Rajan used this opportunity to set for the bank a long-term inflation target. In a previous review, it had been announced that the RBI was focussed on targeting a 6% inflation rate by January 2016, and that conversations were on between the RBI and the Government regarding setting a formal inflation target.

In today’s review, Rajan took this one step further announcing that after January 2016, the RBI will set its policy rate targeting an inflation rate of 4% +/- 2%. This is extremely significant for for the first time it signifies a primarily inflation-targeting objective for the Reserve Bank of India. Over the last few months Rajan has made several attempts to explain that low and stable inflation is a necessary condition for a high and stable growth rate, and having primed us with this narrative, he has finally committed to a long-term inflation target.

The second important takeaway was the emphasis on consistency in policy. Rajan mentioned that while he is prepared to cut rates when the conditions are ripe, what he doesn’t want to do is to flip-flop on rates. This means he is likely to cut rates in this policy review only if he is confident that the requirement of having to raise rates in the next policy review is going to be low. This is extremely significant, as this kind of a direction is an implicit commitment to both savers and borrowers that they can expect the same direction for a significant amount of time, which means that they can plan better.

While some commentators might be disappointed that rates were not cut today, I think today’s policy review was extremely fruitful and some of the commitments made will have important consequences in the long run. Consistency in policy is an extremely important step, and the adoption of a formal inflation target at a time when global oil and food prices are dropping is excellent timing.

The press conference itself was quite insightful, and the way Rajan and his deputies handled the questions was extremely instructive. For example, one journalist mentioned that we’ve already hit 6% inflation which was the target for January 2016, and asked why rates weren’t cut on that account. Rajan replied that the fact that inflation is 6% today doesn’t imply that it will stay there a year later, and we need to work towards holding it there, and that the holding of rates in today’s review was a step in that direction.

Exponential need not mean explosive

Earlier on this blog I’ve written about the misuse of the term “exponential” when it is used to describe explosive increase in a particular number. My suspicion is that this misuse of the word “exponential” comes from Computer Science and complexity theory – where the hardest problems to crack are those which require time/space that is exponential in the size of the data. In fact, the entire definition of P, NP and NP-completeness have to do with the distinction between problems that take exponential resources versus those that take resources that are a polynomial function of the size of data.

Earlier today, I shared this blog post by Bryan Caplan on Puerto Rican immigration into the United States with a comment “exponential immigration”. I won’t rule out drawing some flak for this particular description, for Caplan’s thesis is that Puerto Rican immigration took a long time indeed to “explode”. However, I would expect that the flak I get for describing this variable as “exponential” would come from people who mistake “exponential” for “explosive”.

Caplan’s theory in the above linked blog post is that immigration from Puerto Rico to the United states was extremely slow for a very long time. It was in the late 1890s that a US Supreme Court ruling allowed free access to Puerto Ricans to the United States. However, it took close to a hundred years for this immigration to “explode”. Caplan’s theory is that the number of people moving to the US per year is a function of the number of Puerto Ricans who are already there!

In other words, the immigration process can be described by our favourite equation: dX/dt = kX, solving which we will get an equation of the form X = a exp(kt), which means that the growth is indeed exponential in time! Yet, given a rather small value of X_0 (the number of Puerto Ricans in the United States at the time the law was passed), and given a small value of k, the increase has been anything but explosive, despite it being exponential!

The point of this post is worth reiterating: the word “exponential”, in its common use, has been taken to be synonymous with “explosive”, and this is wrong. Exponential growth need not be explosive, and explosive growth need not be exponential! The two concepts are unrelated and people would do well to not confuse one with the other.

Compounding and Foreign Policy

In today’s Business Standard, Nitin Pai writes about something he’s mentioned a few times before – that India’s best China/Pakistan/US policy is “8% growth”. Unfortunately a lot of space in his piece talks about appointments in ministries and cabinet formation, and he doesn’t directly touch upon why 8% growth is a viable foreign policy (it is possible he had mentioned this but got edited away).

There are two primary reasons why strong economic growth makes for good foreign policy. Firstly, a fast growing economy means that others will want to get their share in it. If you are growing at a rate much higher than the other big economies, other countries will want to piggyback on your growth. They will want to trade with India, invest in India and get India to invest in their respective countries. And for any of this to happen, the foreign country will need to have an overall good relationship with India – if they piss off India, they can get left out of partaking in India’s economic growth. And that will ensure good foreign relations.

The second reason has to do with compounding. Assuming that India can afford to spend only a fixed percent of its tax revenues on defence (being a democracy, the government will always have commitments towards welfare and infrastructure spending which cannot be touched), and assuming that taxes as a proportion of GDP are constant, this means that India’s defence spending is likely to be proportional to the GDP.

With 8% growth, India’s real GDP expected to double in about 9 years’ time. Or, our defence budget can double in 9 years’ time. With only about 5% growth (as we have now), in 9 years our GDP, and consequently our defence budget, will only increase by 50%! That is the power of compounding, and that shows you how increased economic growth can lead to greater defence spending, by keeping proportion of defence spending constant!

Analyzing Bangalore’s Growth

Banglore’s population has grown 20-fold and area 10-fold since 1941, going by this chart (via Gautam John on Facebook, photo taken at MG Road Metro station).

What would be interesting to see is when the spurt in Bangalore population actually happened. Checking that is quite simple. Using the population figures from the census, we can derive the CAGR (compounded annual growth rate) of the population in each decade. This is presented in the chart below:

Conventional wisdom is that Bangalore was a sleepy little city until the “IT revolution” happened around the turn of the millennium after which the city exploded. The chart above calls that wisdom into question. While the annual growth rate of Bangalore’s population has been higher in the noughties compared to the earlier two decades, this is by no means the period of Bangalore’s fastest growth.

Bangalore grew fastest in the 1940s, perhaps because it was made capital of Mysore State after independence, thus leading to the arrival of a large number of government servants in the city. Interestingly, the next period of high growth in the city was in the 1970s, which was even before the seeds of the IT revolution had been sold (the setting up of the Texas Instruments office in Bangalore in the early 80s is regarded as the beginning of Bangalore as an IT hub).

What might have led to the perception of Bangalore’s growth being fastest in the noughties is that the strain on a city’s infrastructure is a superlinear function of the city’s population. And with a lot of the city’s infrastructure having been stagnant over the years, the strain started getting really noticed in this decade.

Growth in India’s foreign trade

I was looking at data from the 2012-13 Economic Survey, and was looking at India’s imports and exports over the year. Just the sheer pattern of increase in trade was stunning, so I thought I should graph it and share it here.

Offered without further comment:

Accuracy of GDP Numbers

Earlier today on Twitter, RahulRG pointed out a research report by Credit Suisse analysts Neelkanth Mishra and Ravi Shankar which talks about India’s massive informal economy. The report says that by nature the informal economy cannot be measured, because of which our estimates of GDP may not be accurate. The analysts point out that every time we move to a new series of GDP (we last did so in 2004, and are likely to do so again shortly), there is an upward revision in the GDP for the preceding series, which they attribute to underestimation of the contribution of the informal sector.

While these numbers are likely to get fixed when we move to a new series, what I’m concerned about is what this uncertainty in GDP estimation means with respect to the GDP growth rate, since that is the one number that analysts of all hues track when trying to understand how the country is doing. For example, if you google around you will see analysts arguing about whether India’s GDP growth in the next quarter will be 4.7% or 4.8%. Before we settle to argue on such minutae, I argue, we first need to understand the possible uncertainty in GDP estimates.

In order to estimate the impact of uncertainty of the GDP calculation on uncertainty in GDP growth, I did what I know best – a simulation. For different levels of accuracy, I calculated the range that the actual GDP growth can take. The results are presented in the following table. The first column in the table refers to the accuracy of the GDP estimate at the 95% confidence level. That is, if the first column shows 1%, it means that if the GDP is estimated to be 100, the “true” value of the GDP will be between 99 and 101 95% of the time.

Error	True GDP Growth Rate
Error	5%	6%	7%	8%
0.05%	4.93-5.07	5.93-6.07	6.92-7.08	7.92-8.08
0.1%	4.85-5.15	5.85-6.15	6.85-7.15	7.85-8.15
0.2%	4.7-5.3	5.7-6.3	6.7-7.3	7.69-8.31
0.5%	4.26-5.74	5.26-6.75	6.25-7.76	7.24-8.77
1%	3.54-6.49	4.51-7.52	5.5-8.52	6.48-9.53
2%	2.09-8.03	3.03-9.02	4-10.05	4.98-11.13

Notice that even if the measurement of the actual GDP is accurate up to 0.05% (or 5 basis points), we can estimate the growth in GDP only up to an accuracy of 15 basis points! So arguing whether the GDP growth will be 4.7% or 4.8% is, in my opinion, moot! Unless our statisticians can say that the accuracy in measurement of the GDP is within 5 basis points that is!

PS: Also read Neelkanth Mishra’s excellent op-ed in the Indian Express on India’s informal economy.

Strain on Indian Railways

In my last post I looked at some railways data that was put out by the Economic and Political Weekly to show that the total addition in route length over the last 20 years is not much to talk about. The same data set also gives data on “passenger kilometers” and “passenger train kilometers” for each year. The latter gives the total distance all passenger trains in India have run, while the former gives the total distance traveled by (ticketed) train passengers in India each year.

Now, the ratio of these two numbers gives us the number of passengers per train. It is interesting to note how this has moved in the last 20 years.

Data source: Economic and Political Weekly May 18, 2013 vol xlviII no 20

In 1990 the average train used to carry about 800 passengers. That number has almost doubled to 1400 in 2009 (data on passenger train kilometers not available after that).

While some people might see this as a measure of higher efficiency by the railways, I see it more as an inability by the railway infrastructure to keep up with passenger demand. With little track length having been added, there is no surprise in that.

Growth in Per Capita Consumption Expenditure

Measuring people’s incomes is a hard task. There is considerable incentive to both under and overestimate one’s own income while responding to a survey. Thus, a good proxy for measuring incomes is to look at the total consumption expenditure.

One of the assignments for the ongoing batch of the Graduate Certificate in Public Policy Program asked them to analyze how the quality of life in India has changed over the last 50 years. Rishabh Raj responded to the assignment with the graph that is presented below, that shows how the per capita consumption expenditure has grown over the last 50 years. Note that the figures are adjusted for inflation. Offered without further comment:

Source: http://data.worldbank.org/country/india Numbers in 2000 rupees.