Recently on this blog I had talked about the phenomenon of correlations, and how that can send financial models topsy-turvy. I had taken the example of additional cars on the road on a rainy day and had explained how in 2008 CDOs went bust as a fall in house prices led to mortgages defaulting together. Today I read this interesting post by JP Koning which attributes the stock market crash of 1987 (Black Monday) also to correlation, but of a different kind.
It basically have to do with how bubbles behave. When you know that the stock market is overheated, there are two things you can do. You can either choose to ride whatever is left of the bubble, and thus go long, or short the market and hope that the bubble has come towards its end. There are problems with both approaches – if you are long and the bubble bursts, you stand to lose significant money. On the other hand if you are short and the bubble continues, you can end up getting wiped out before the bubble bursts and offers you an opportunity to profit (as Keynes supposedly said – the market can remain irrational for longer than you can remain solvent).
Trading is difficult business during the times of a bubble. Every good trader knows that a bubble is on. Yet, they are faced with the above dilemma. They want to participate in the party as long as it lasts but leave before the house comes crashing down. But nobody knows when the house will crash. Some smart traders such as Taleb (no doubt backed by their banks’ deep pockets) simply buy put options and wait it out for the bubble to burst and make their money. Some get out of the market. But most remain, taking directional bets (in either direction) and not sure of whether they are going to get wiped out.
Suppose you are a trader in one such bubble, and you decide to use a mixed strategy of whether you go long or short. Let us assume that on four out of five days (randomly chosen) you are long the market, and you short the fifth day. Let us assume every trader follows a similar strategy, but strategies of no two traders is correlated. So on a given day, for every trader going short, there are four traders going long and thus the bubble continues (let us assume that each trader plays with the same amount of money). You can see where this is going. What if there is a day when for some reason more than the usual 20% of the traders decide to go short?
Let us briefly revisit the house party analogy. There is a party on and you want to enjoy it for as long as possible. However, the house in which the party is going on is unstable, and as soon as the number of people in the house falls below a certain number, the house will collapse, crushing anyone still in there (yes, this is a weird house, but never mind). You go near the house and you see a large number of people having a gala time. You see that the number of people in the house far exceeds the threshold, and so you join the party. And thus the party swells.
Suppose you are now in the party, and you see a large number of people leaving. Suddenly, you realize that following their exit, the number of people left in the house will be not too much more than the threshold. If you stay on, you might end up holding up the house, you might reason, and you will want to leave with the large group. The only problem is that you are not alone in thinking such. Most other guests have also seen this large group leave, and want to accompany them on their way out.
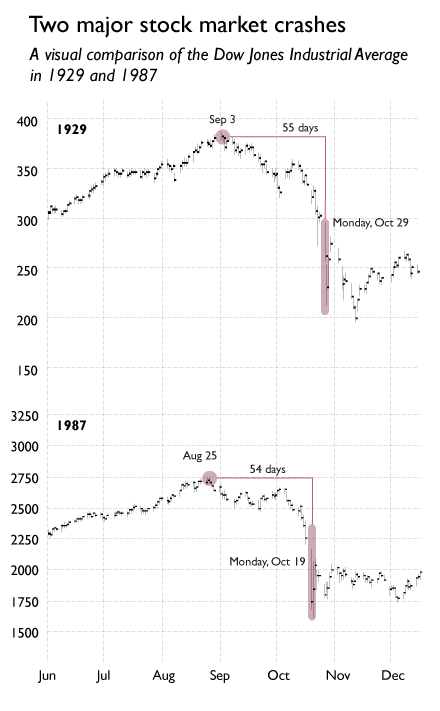
Traders were aware that the crash of 1929 had also occurred in late October, and on a Monday. On the 19th of October 1987, Koning mentions in his blog, the Wall Street Journal published a graph of the stock market in the 1980s and superimposed it with a graph of the stock market in the 1920s, leading up to the stock market crash in 1929 (which led to the Great Depression). The two graphs looked similar, as you can see below.
This was all the trigger that the market needed. Suddenly, you have a day when every trader reads about the bursting of the 1929 bubble in the newspaper, and how the current market is similarly poised. Suddenly every trader is doubly conscious of the stock market bubble, and wants to get away. Instead of every trader playing a random strategy, where only 20% will want to short, on this particular day a much larger number of traders want to short. As they collectively short, the market falls significantly enough to tell everyone that the bubble is busting. Everyone else tries to join them as they try to rush out of the party house. The house duly crashes.
Once again, notice that this was a random system being held up by low correlation. Traders knew there was a bubble, but didn’t know when it would burst and thus played uncorrelated mixed strategies, which kept the market afloat. All it took was one newspaper article, which every trader happened to read. The correlation suddenly jumped, and the market moved decisively.
As an exercise at the end of this blog post, think of other systems which are similarly “held up” because of low correlation in people’s behaviour. It need not only be financial – remember the road on rainy day example I gave in my previous post. Then think of what might result in correlations that hold up these systems to collapse to 1, and how those systems will then respond. Please don’t, however, blame me for scaring you.
Runs on a retail bank
Depend on all depositors not pulling out money at once v